[最も人気のある！] 等差数列の和 シグマ 209240-等差数列の和 シグマ

 大学受験において頻出単元の1つである「数列」。 公式や考え方をしっかりと覚えて、確実に得点していきたい単元だ。 等差数列や等比数列の一般項だけでなく、数列の和の計算についても紹介。 さらに、Σ（読み方は「シグマ」）の公式や計算方法、階差数列や漸化式の基本についても説明していく。 数列に関して基本をおさえられる記事になっているので等差数列とその和 ・等差数列の隣接する項の関係を考 察し、その一般項や第n項までの和 を求めることができる。 ・一般項を表すことができたか。 ・等差数列の和の公式を理解し、そ れを適切に利用で等比数列の和 等比数列の公式はジッと見ていても何を言っているのかわからない。 ここでは公式をどのように導いているのかと、導く上でのコツを紹介するぞ！ はじめに、Σとは何をしているのか思い出しましょう。 Σとは、 「a1からan a 1 か ら a n まで

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

等差数列の和 シグマ

等差数列の和 シグマ-等差数列の和の成 り立ちを，記号や数 式，視覚的な情報を 用いて的確に表現 している。 4 ・等差数列の和の公 式を適切に利用し て，等差数列の和 を求める。 ・自然数の和，奇数の 和，倍数の和など を求める。 則性を知る。 ・等差数列の和 を表現する 例えば次のような等差数列、1、2、3、4、 、9、10の和は、 $$1234cdots910$$ と書けますが、これを省略しようと思ったときに登場するのがシグマ

48s96ub7b0z5f Net Tousakakerutouhi

等比数列の和にはシグマの計算公式が使えない シグマ（Σ）は和を表す記号で、公式では無いということは何度も言ってきたのでわかっていると思いますが、 計算公式も3つだけはあるというのも知っていますよね。 \displaystyle \sum_ {k=1}^n k=\frac {1} {2}n (n1) \displaystyle \sum_ {k=1}^n k^2=\frac {1} {6}n (n1) (2n1) \displaystyle \sum_ {k=1}^n k^3=\left\ {\frac {1} {2}n右辺を等比数列の和の公式で計算する： (1x)S_n=\dfrac {x (1x^ {n})} {1x}nx^ {n1} (1−x)S n = 1−xx(1−xn) − nxn1 ですので等比数列の和の公式を使って、 初項3、公比2、項数 n より ∑ k = 1 n 3 ⋅ 2 k − 1 = 3 ( 2 n − 1) 2 − 1 = 3 ( 2 n − 1) と計算できてしまうわけです。 一般的に書くと ∑ k = 1 n a ⋅ r k − 1 = a ( r n − 1) r − 1 です。 a 、 r 、はそれぞれ 初項、公比 に当たります。 公式は便利ですが、最初のうちはすこし書き出して 等比数列の和であることを確認してから計算する

等差数列（一般項） 1631 3．等差数列（和） 941 4．等比数列（一般項） 1731 5．等比数列（和） 1044 6．等比数列の和の公式の使用例 748 7．ジグザグ型の数列 537 8．調和数列 215 9．シグマの意味 1245 10．シグマの公式 849 11．階差数列（一般項 今度は、一番奥の括弧からシグマ計算をしていきます。等差数列の和の公式から使っていきます。 解説と照らし合わせてみてください。 内側から順に、 等差数列の和の公式 →シグマの分配法則 →2乗和と1乗和 →mについて整理 等差数列のときと似たような導入でかきます。覚えなくていい「等差数列の和」 算数は得意なのに数学が苦手なひとのためのブログまず、等比数列の公式として、 こんな感じで教わってるかな？ それとも みたいな感じ？ こんな感じで覚えてると、は？

B F N K E X ̕ @ @ K E X i h C c ̑吔 w 1776 `1855 j N ̍ C w Z ̐搶 如果等差数列的公差 \(d0\) ，正数之和一定为正，并且只要是正数，则正数相加的个数越多，其和越大； ↩︎（位相が等差数列なら）複素指数関数と等比数列の和の公式を用いて三角関数の和を計算することができる： ∑ k = 0 n sin ⁡ ( θ k ϕ ) = sin ⁡ ( ( n 1 ) ϕ 2 ) sin ⁡ ( θ n ϕ 2 ) sin ⁡ ϕ 2 \displaystyle\sum_{k=0}^n\sin(\thetak\phi)=\dfrac{\sin(\frac{(n1)\phi}{2})\sin(\theta\frac{n\phi}{2})}{\sin\frac{\phi}{2}} k = 0 ∑ n sin ( θ k ϕ ) = sin 2 ϕ sin ( 2 ( n 1 ) ϕ ) sin ( θ 2 n ϕ )

数bの等比数列の和と シグマ の違いを教えて下さい Sは Yahoo 知恵袋

数学の質問です 写真のsの数列の和の公式が とても複雑でやや Yahoo 知恵袋

 Σ（シグマ）は、数列の和を簡潔に表すための記号 Σ（シグマ）の2つの性質 Σ（シグマ）で和を簡潔に表せるからこそわかること・見えてくるもの 等差数列の和は、1からnまでの和を知っていれば計算できる nの2次式で表される数列の和は、2乗の和をどちらもシグマを展開して書き並べて， 公比をかけたものを右にずらして引きます． (1)で説明すると 上のように，引き算を実行すると， 等比数列の和が現れて (解答波下線部) ， Sn S n を求められます． (2)の (2次式)× (等比)の和の方は，1回この操作を行うと (等差)× (等比)の和になります． 解答 (1) ∴ Sn = (2n− 1)2n1 2 ∴ S n = ( 2 n − 1) 2 n 1 2 (2) ∴ T n = (n2 −2n 和の中抜けとは？ 分数や連続整数の積の総和を求める方法を例題付きで紹介！ 1 和の中抜けとは 12 数列の総和の公式が使えないときに和の中抜けは有効 2 和の中抜けが有効な例3

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

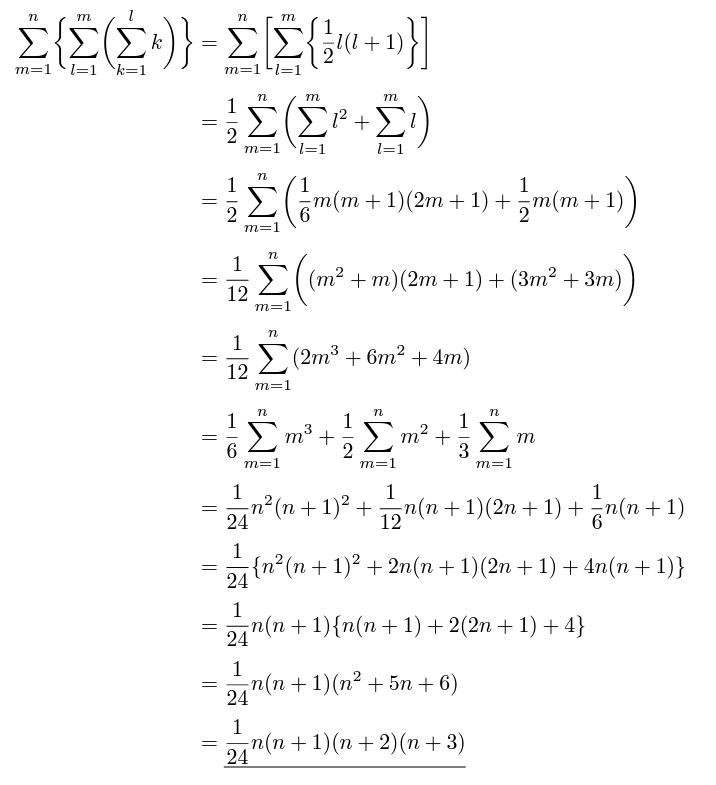
等差数列や等比数列とシグマ計算s 大学受験対策にも タロウ岩井の数学と英語 Note

よって，2S10=24×10=240 より S10=1 となります。 一般に，初項 a，公差 d，項数 n の等差数列の末項を としますと，初項から第 n 項までの和 Sn は， Sn=a (ad) (a2d) (d) (3) となります。 また，S10は上の例と同様に， Sn= (d) (2d) (ad)a (4) と書けますので， (3)と (4)の辺々加えますと，等差数列の和 1からウン千までのランダムな整数を並べたデータに、被りや欠落が無いかを確認するために利用させていただきました。 お年玉 (年齢×1000)の総額計算に！ 1から397までの和を求めるため、等差数列計算を利用。 等差数列をなす3つの数をもとめるため。 アンケートにご協力頂き有り難うございました。 送信を完了しました。 アンケートは下記にお 等差数列・等比数列とその和 まず最初は数列の一番簡単な形である 等差数列 と 等比数列 について学習します。この2つは数列を考える上で避けては通れません。数列の規則性とその一般項、数列の和の求め方などを覚えます。

高校数学b 等比数列 A N の和 １ 映像授業のtry It トライイット

48s96ub7b0z5f Net Tousakakerutouhi

Try IT（トライイット）のΣ と等差・等比数列の和の例題の映像授業ページです。Try IT（トライイット）は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る（トライイットする）ことにより「わからない」をなくすことが出来ます。・等差数列：等間隔で並んでいる ・等比数列：等倍率で並んでいる ・階差数列：元の数列の差をとったもの ・分数 → 分母や分子に規則性 ※ 調和数列：等差数列の逆数となっているもの ・フィボナッチ数列：前2つの数字を足したもの （1,1,2,3,5,8,13, ） 今講座で学ぶ内容は2つあります。 一つ目はシグマ記号を用いた計算です。 これを学習すると、これまでに学習した等差数列と等比数列以外の和も求められるようになります。 二つ目は「階差数列」です。 「1、2、4、7、11、16、」という数列の続きはわかりますか？

高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月

シグマの計算 苦手になるポイントを徹底解説 家庭教師の想い

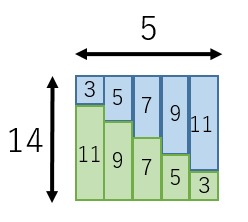
 等差数列の和（具体例） 次のような等差数列を考えてみましょう。\ 1,4,7,10,13,16,19 \これは、初項が $1$ で、公差が $3$ 、項数が $7$ の等差数列です。この数列の和を考えてみましょう。 もちろん、前から順番に足していく、という方法もあります。和の公式へのアプローチ 札幌旭丘高等学校 吉田 奏介 1 2 3 l n の場合 まず教科書ではどうだろうか。等差数列の和のところで次のような説明がなされている。 等差数列の和の公式の導入に際し図を用いているが，自然数の和は公式の延長線上としてとら 第3講 等差数列の和 等差数列の総和は基本的内容ですが、スムーズに計算できなければ入試では通用しません。 試験でも通用する計算の仕方を学びましょう！

数列の和とシグマの公式を成り立ちから徹底解説 暗記から理解へ

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

 数列の和とΣ(シグマ)記号の意味と使い方 ＊この記事では、$$等差数列の一般項a_{n}=a_{1}d( n1)と $$ $$等比数列の一般項a_{n}=a_{1}\times r^{n1}$$ は既知として、Σ公式やその証明などを解説していきます。等比数列の和の公式について質問させてください。 先生のページでは、項比rから－1するという形になっていますが、 別の書籍等では、1から項比rをマイナスするという形になっているものもあります。 この違いは何に起因するのでしょうか？でも、このシグマの中身が、初項 、公比 の等比数列の一般項だとわかると、等比数列の和として一気に計算できる。なんでわかるねん！という方は、シグマを書き下してみるとわかる。 証明 は等差数列 なので、初項 、公差 の等差数列の和として計算

3

高校数学b 絶対値付き数列の和 S A K 受験の月

 等差数列の和の公式 等差数列の和 S n = ∑ i = 1 n a i は以下のように書き換えられる。 (2) S n = 1 2 n ( a 1 a n) これが等差数列の和の公式だ。 ガウス君の問題だと、 n = 100, a 1 = 1, a 100 = 100 なので、 S 100 = 1 2 100 × ( 1 100) = 5050 というように、公式 (2)を使えば

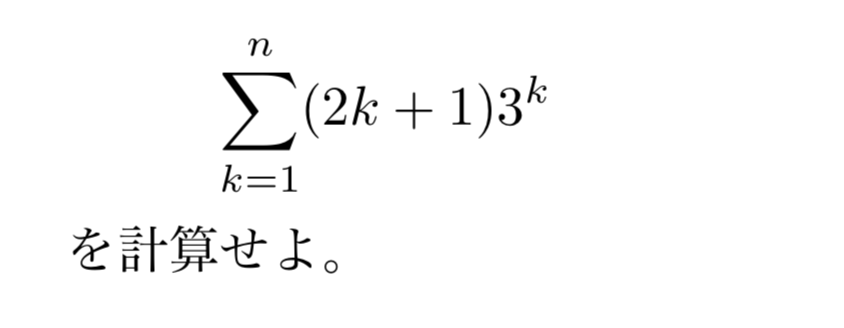
和の中抜けとは 分数や連続整数の積の総和を求める方法を例題付きで紹介 東大医学部生の相談室

高校数学b 応用的なs計算 第k項にnを含む数列の和 和の和 受験の月

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

等差数列や等比数列とシグマ計算s 大学受験対策にも タロウ岩井の数学と英語 Note

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 5 8

シグマ特講 第３講 等差数列の和 東大医学部の解説動画 Youtube

シグマ記号sの考え方 数列の和を表すsの定義と性質

等比数列の一般項と和 おいしい数学

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

数列と級数 京極一樹の数学塾

例題で学ぶ高校数学 階差数列

数列 奇数の和 を求める 大人が学び直す数学

高校数学b 等差数列の和s Nの最大値の問題 映像授業のtry It トライイット

高校数学b 等比数列の一般項 A N Ar N 1 受験の月

等差数列や等比数列とシグマ計算s 大学受験対策にも タロウ岩井の数学と英語 Note

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

階差数列

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等差数列 シグマの和 この手の問題の共通の箇所をくくるというところが Yahoo 知恵袋

等差数列や等比数列とシグマ計算s 大学受験対策にも タロウ岩井の数学と英語 Note

センター数学裏技 等差 等比の和を10秒で求めるチート級裏技 高校数学 お笑い数学教師 タカタ先生 超わかる 授業動画 Youtube

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

数学b 数列 和から一般項を求める オンライン無料塾 ターンナップ

等差数列の和を計算する2つの公式 具体例で学ぶ数学

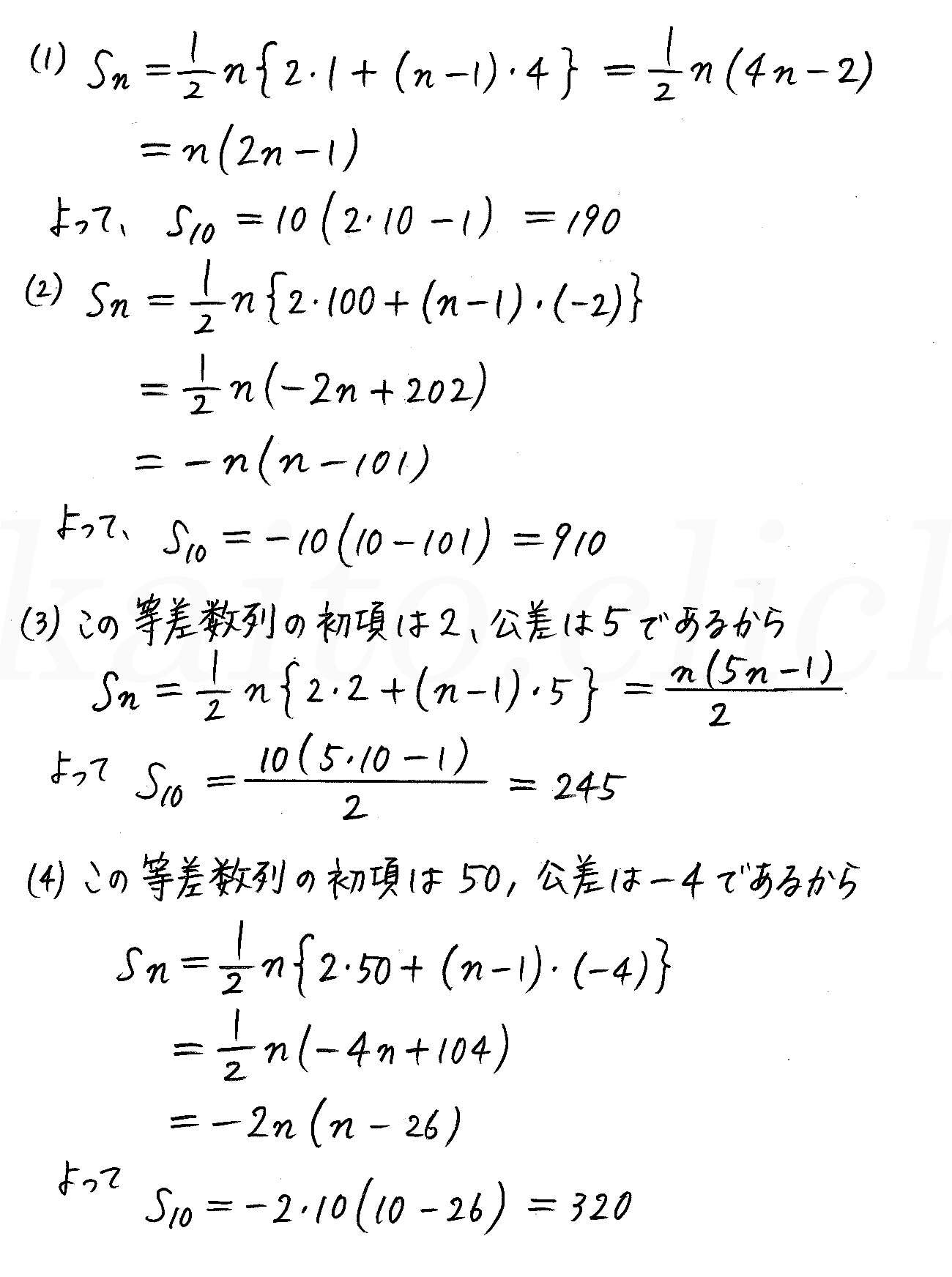
改訂版 クリアー数学b P149 15 等差数列の和

48s96ub7b0z5f Net Tousa Suuretsu

Q Tbn And9gcrhoqs Tiaw74o0thwqpqqyulvy4xv5hy7apwesqqy4i H6wzaw Usqp Cau

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

力をつけよう２ S 等差数列 等比数列 力をつけていいんじゃない

階差数列の全てをわかりやすくまとめた 公式 漸化式 一般項の解き方 理系ラボ

シグマがわからななくて調べていたらこのような式が出てきたのですが どういうことなので Clear

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

等差数列の和とシグマの計算方法

和を求める時 左の問題はなぜ Sを使うのですか Clear

数列の和とs記号 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

階差数列

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

1乗和 2乗和 3乗和の公式 導出法から理解しよう

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

数列の和の一問一答カード 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

最後のオカキの質問です どうして等差数列の和の形になっているので 数学 教えて Goo

等差数列の和 ｓₙ ａ ａₙ ｎ ワンセンテンス算数 Note

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

高校数学b 等差数列と等比数列の共通項の数列の一般項 受験の月

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

高校数学b 階差数列から一般項を求める １ 練習編 映像授業のtry It トライイット

等差数列と等比数列の積の和の問題の解法ポイント 数列

1 の問題が 解説を見ても意味がよくわかりません Tt シグマの計算は分かるのです Clear

分数の数列の和 高校数学ｂ Youtube

和の記号s シグマ の公式と 証明方法 高校生向け受験応援メディア 受験のミカタ

等差 等比 の和 2次式 等比 の和 おいしい数学

等比数列の和の公式を利用するs シグマ の計算方法を解説 わかるようになる高校数学

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

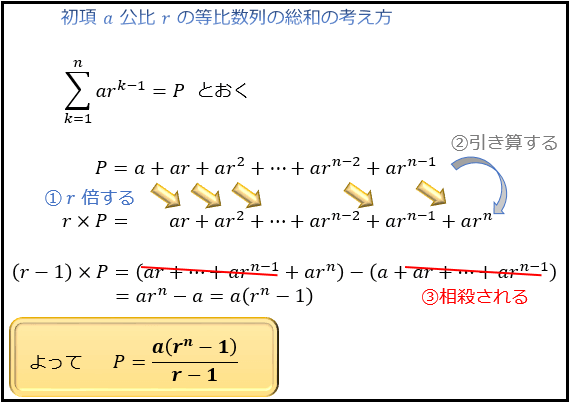
総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

高校数学b Sの性質と数列の和の公式 S公式 Sk Sk Sk 受験の月

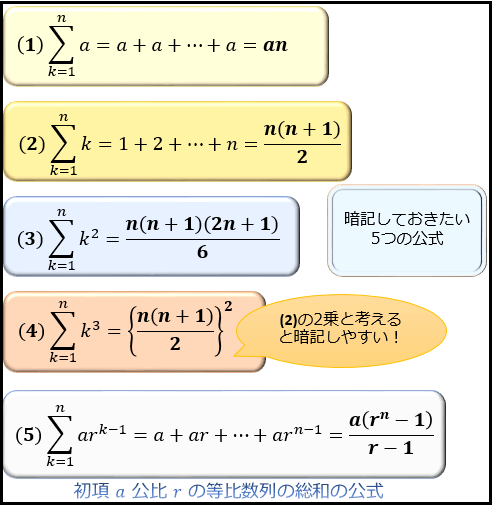
総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

等差数列 等比数列の和はs Rsで求められるのは理解したのですが Yahoo 知恵袋

数列の基本２ 等差数列の和の公式 と 等比数列の和の公式

等差数列の和の最大 数学b 等差数列と等比数列 5 Youtube

数学用語解説

高校数学b S と等差 等比数列の和 練習編 映像授業のtry It トライイット

高校数学b 等差数列の和s Nの最大 最小 受験の月

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

48s96ub7b0z5f Net Shigumanokeisan

和の記号s シグマ の公式と 証明方法 高校生向け受験応援メディア 受験のミカタ

写真の水色の線のところなんですけど見えにくかったらすみません 下の２行です Clear

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

等差数列の和とシグマの計算方法

数列の問題でシグマと部分分数分解を応用 した問題の解説を求めます Yahoo 知恵袋

これでわかる 数列のシグマsの計算方法を徹底解説

高校数学b S と等差 等比数列の和 映像授業のtry It トライイット

高校数学b S と等差 等比数列の和 練習編 映像授業のtry It トライイット

階差型の数列 おいしい数学

Catatan Tentang 詳説 数学ｂ 等差数列 等比数列 Senior Clear

1

3

和を求める時 左の問題はなぜ Sを使うのですか Clear

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

等差 等比 の和 2次式 等比 の和 おいしい数学

高校数学b S と等差 等比数列の和 練習編 映像授業のtry It トライイット

等差数列の一般項と和 おいしい数学

等比数列 循環数列とその和

Sシグマの公式まとめと計算方法 数列の和の公式 理系ラボ

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

このように初項と公差と末項が分かっている時にはどうやって解いたらいいのですか Clear

階差数列

数列の基本５ 階差数列の考え方は簡単 階差数列の公式

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

Incoming Term: 等差数列の和 シグマ,